中国粉体网讯
离散元法的优点
在上世纪七十年代,美国研究专家Peter Cundall提出了离散元法(Discrete Element Method,DEM)。该方法是模拟研究大量离散颗粒物质运动行为和细观分析最为有效的方法,可以获得颗粒物质内部各种复杂的信息。
DEM最先在研究水泥的堆积过程中得到了成功的应用。随后,离散元法被广泛的应用于颗粒物质和粉体的研究中。与颗粒物的连续介质理论相比,离散元模拟具有以下优点:
一是在研究工业生产设备中颗粒物体运动行为缺乏可靠理论的情况下,可以先用离散元模拟来分析结果,然后设计和优化设备;其次,更大规模的实验通常是昂贵的、耗时的,甚至是危险的,基于离散单元法的仿真模拟实验可以作为相关物理实验的补充与替代,同时结合仿真中的工具可以更方便地计算与测定出实验目标数据,进而完善现有理论,更好地解决实际工程问题。同时,离散元法可以通过牛顿第二定律对各个粉体颗粒单元之间的接触碰撞进行实时反馈与计算。
其作为一种新的数值模拟计算方法,为粉体力学以及微观力学等领域的研究提供了有效途径,有着非常广泛的应用前景。在制药领域,其可以模拟仿真制药过程,包括制粒过程、滚压过程、物料输送、混合等生产工艺,因此广受制药企业和研究者青睐。
离散元法的假设和简化
由于颗粒通常具有一定的形状尺寸和重量,在离散元法中为了便于分析和研究,通常对模型进行一定程度的假设和简化。在离散元法中,主要存在以下几个假设:
(1)颗粒材质是刚性的,对于研究颗粒,其接触受力产生的整体变形是由所有接触变形叠加形成的;
(2)颗粒间的接触一般可以看成为点接触,其接触面积非常小;
(3)相邻颗粒间在接触处存在一定的重叠量,该重叠量要远远小于颗粒单元的粒径;
(4)在每一研究时步内,待研究颗粒只可能与其周围颗粒发生接触,不能跨多网格产生接触。
虽然离散单元法的算法简单易行,但是由于颗粒实际形态的复杂性,在离散元方法中很难对颗粒的真实形状进行模拟,而且模拟计算量与颗粒数量密切相关。在不产生显著误差的情况下,通常对颗粒进行一定程度的简化,采用圆盘或圆球形颗粒。
为了更接近颗粒的实际形态,在模拟研究的过程中对颗粒的实际运动情况进行分析,一些研究人员采用了椭圆或者椭球形颗粒,但是接触搜索及判断则变得更加复杂,程序实施变得更加困难,模拟计算时间也成倍增加。借鉴微积分的思想和发展历史,离散元法作为一种近似数值解法的科学方法,能够在一定程度上反映颗粒物质运动问题的本质。
离散元法的工作原理
离散单元法是通过求解牛顿第二定律和接触模型,在迭代时间步长上模拟单个粒子的速度、位置和运动等力学动力学的数值方法。其主要工作原理包括:
1)在时间步长内模拟跟踪每个颗粒单元的轨迹,以评估其具体位置和运动方向;2)根据牛顿第二定律,采用迭代法(静态松弛法和动态松弛法)对单位时间步长内的颗粒单元的运动和受力进行计算求解,再根据中心差分法对质点的运动方程进行数值积分,进而求解出单位时间步长附近的颗粒更新后的速度和位移,计算出颗粒单元之间的相互作用以及颗粒单元与环境之间的相互作用,经过不断地迭代计算来更新颗粒单元的受力和运动情况,最后通过计算和追踪每个颗粒单元的受力、运动情况来得出系统颗粒流的宏观运动规律。
基于软球模型的离散元法
尽管目前关于颗粒物质运动的研究已经十分完善,但是在实际分析研究的过程却极其复杂。为了提高研究效率并且保证研究准确,研究人员对研究内容和方式进行了简化,提出了两种模型,即软球、硬球模型。
在软球模型的分析研究中,物质间的相互作用是一个连续的过程。在该简化模型的分析中对于所要研究的颗粒物质表面的变形进行了忽略,软球模型的研究对颗粒间力的具体加载历史不予考虑,适合于工程中较为密集的颗粒系统的数值计算,目前大多数离散元的模拟计算都是基于软球模型进行的。
与软球模型不同,在硬球模型的分析中认为物质间的相互作用是在极短的时间内完成的,依据选取的模型快速计算出发生接触后物质运动行为的变化。颗粒物质间的恢复系数影响接触碰撞过程两颗粒的能量变化。硬球模型通常用来研究运动速度快、颗粒物质浓度不高的颗粒体系。
颗粒接触模型
离散元法模拟研究颗粒和粉体的运动特性和细观行为,相邻颗粒之间相互接触碰撞存在力的产生。每个颗粒的具体运动特征与所选取的颗粒接触模型密切相关。因此,接触模型在离散元法中极为重要,模型的选取决定离散元模拟的精细程度和正确性,而且粒子的受力情况是通过所选取的模型经过计算得到的。
对于不同的研究物质,需要根据实际工况建立相对应的模型。离散元法经过几十年的发展,在进行分析研究时可供选择的接触模型有多种,既有分析研究颗粒物质运动状况的模型,也有分析大块物质受力破碎时的粘结模型。
在运用离散元法进行研究问题时,Hertz-Mindlin无滑动接触模型是最基础也是使用最广泛的模型,能够反映大多数工况下待研究物质的情况。该模型是通过对Mindlin研究内容进行一定程度的修正完善之后得以建立的。在该模型中两颗粒发生接触的变形如下图所示(图中α为法向重叠量,δ为切向重叠量,虚线是不考虑变形时颗粒表面所在位置)。
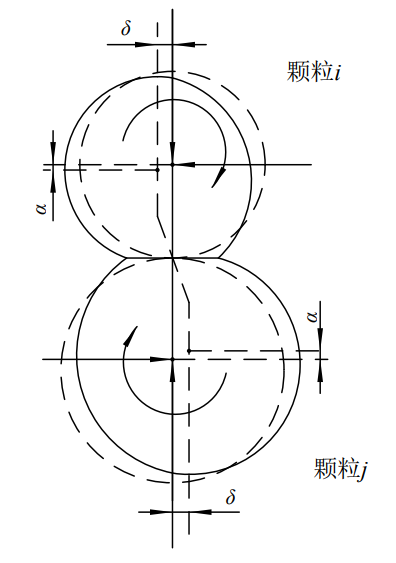
颗粒接触变形示意图
小结
随着离散元方法的提出和计算机科学的迅猛发展,离散元数值模拟方法成为研究颗粒和粉体特性的最为有效的方法之一,尤其是在细观特征和力学行为等方面具有突出的优势。此外,采用离散元法可以对那些费用高、较为危险的颗粒进行研究。在粉体工程方面,研究者开始借助离散元法研究粉体的运动特性,离散元法已经成为研究粉体颗粒力学特性和运动规律的可靠的数值计算方法。
参考来源:
[1]何思平:恒流喂料干法滚压控制装置及其关键技术研究,南昌大学
[2]赵艳波:基于EDEM的粉体振动填充特性研究,太原理工大学
[3]许勇:基于EDEM的染料粉体高精度给料结构优化设计,华侨大学
(中国粉体网编辑整理/平安)
注:图片非商业用途,存在侵权告知删除!


















